In our last discussion, we took a look at linear regressions using a marketing example centered around monthly sales. In addition to being able to fit our previous data sales, we’d also backed out a linear fit (with [math] r^2 = 0.965 [/math] that we could use to roughly predict our company’s sales performance in future months. In doing so, we found that being able to accurately model a “random” set of data is helpful, but there are other problems that need a different kind of treatment. For instance, let’s say we want to bake cookies; in the words of the Cookie Monster, “C is for cookie, and that’s good enough for me.”
In our case, we do not want to simply bake cookies…we want to make the most delicious cookies possible! Looking at our recipe, though, we know we can only vary parameters like number of eggs, amount of flour, volume of butter, or the time and temperature at which we bake the cookies in the oven. When all these parameters come together (assuming all other things constant), we’re left with a measurable (albeit subjective) cookie metric: Taste. For instance, if one recipe uses one stick of butter and tastes worse than cookies produced from a recipe with two sticks of butter, then our taste buds will likely tell us that two sticks of butter is a more optimal butter quantity than one stick!
As you can imagine, there are an infinite number of combinations of eggs, flour, butter, temperature, and time. Computationally, we would say that the “parameter space” is very, very large and continuous. Furthermore, the parameter space is a five dimensional space; if we were to visualize a two-dimensional slice of the five dimensional space, we could plot taste as a function of, say, number of eggs and sticks of butter:
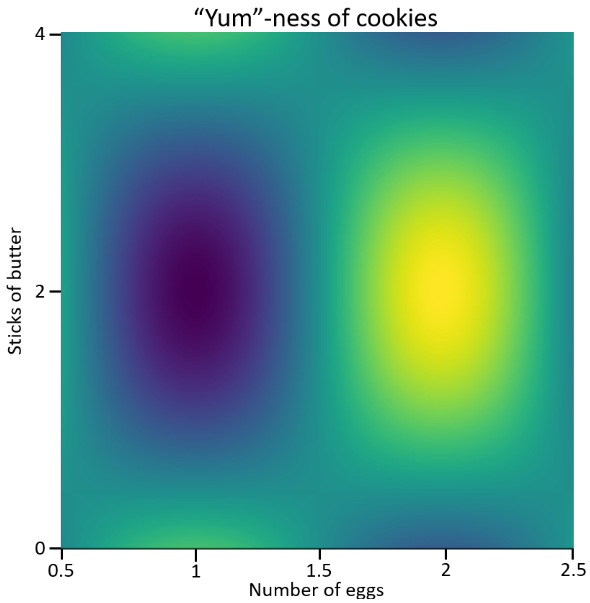
Our map of taste (color) versus number of eggs and sticks of butter seems to suggest that the most delicious cookies occur when we use two sticks of butter and two eggs. Furthermore, if we use too many eggs, our cookies become disgusting. Similarly, too little or too much butter also has adverse effects on the taste of our cookies! As a disclaimer, the map presented above to purely illustrative and is not meant to be used as an actual recipe!
As you can imagine, these type of complex problems can be found all throughout nature. From parameters in building an antenna to the dimensions of an aircraft wing. Ultimately, each of these optimization problems boils down to either minimizing (ex. air drag) or maximizing (ex. taste!) some parameter given many, many options or parameters. We call this computational optimization.
Types of Optimization
Within the field of computational optimization, there only three ways to optimize a function: finitely terminating algorithms, iterative algorithms, and heuristics. The first of these algorithms runs an analysis function on a large parameter space a finite number of times, then stops (hence “finitely terminating”); the answer it reaches at the end is the “optimized” solution we obtain.
On the other hand, iterative algorithms continue to run, crunch numbers, and optimize until a specific condition is met (for instance, when the cookie metric equals Delicious!); when the condition is met, the solution reached by the iterative algorithm is considered our optimized solution. Lastly, heuristic algorithms are algorithms that are not guaranteed to find a solution within a parameter space. These types of algorithms include my personal favorite (and one we’ll look at more in depth): nature-inspired algorithms.
Nature-inspired optimization
The Earth has been around for ~4.5 billion years. In that time, Nature has had plenty of time to come up with some very beautiful and clever routines to solve mathematically complex problems. From ants finding optimal paths to forage for food to a pack of wolves hunting its prey, a list of nature-inspired optimization algorithms contains no less than 338 unique algorithms! This has always fascinated me — humanity’s attempts to understand and mimic the brilliance of Nature. As it turns out, nature is even inspiring artificial intelligence algorithms as well!
Among the more well-known algorithms are:
- Particle Swarm Optimization (PSO)
- Genetic algorithms (GA)
- Ant Colony Optimization (ACO)
- Cuckoo Search Algorithm (CSA)
- Penguins Search Optimization Algorithm (PSOA) (<– not as well known)
So what’s the difference between each algorithm, and why are there so many? This is definitely another topic for another time. For now, though, simply getting our feet wet with a few of these techniques will give us a leg up on understanding the power of these techniques!
Conclusion
In this discussion, we briefly introduced the concept of computational optimization. To gain a better understanding of why it is important, we used cookies to demonstrate how a seemingly simple problem can quickly become very complex. For instance, we examined a two-dimensional cross-section of a five-dimensional parameter space and interpreted its results by eye. Ideally, though, we would not need to do this — we could build a computer program to quickly find the best combination of all baking parameters to arrive at an optimal solution (recipe). In our case, we would expect our software to arrive at the solution that the most delicious cookies are made with two sticks of butter and two eggs!
We then briefly touched on the different kinds of optimization, and took a little detour to talk about heuristic algorithms. Within this realm, we found that there are many nature-inspired algorithms that we can demonstrate in later posts to get a feel for just how powerful these computational techniques can be!
